I have just the opposite problem. To me, some of the notes on a piano sound slightly out of tune as compared to what I play on my violin. I have a similar problem when I play guitar. Depending on which key I am playing in, I have to tweak the tuning a bit to make it sound more in tune.
The crux of this problem is temperament (not of the musician, but of the instrument!). That is, how the musical scale is put together. The musical scale that our western ears are used to hearing is a chromatic scale of 12 semitones or a diatonic scale of 8 notes. Just how those tones are divided is the matter of temperament.
There are certain intervals of tones that are most pleasing to our ears. Those have ratios of frequency that are simple fractions. Those tones are most pleasing because they share the most resonance frequencies or harmonics. For example octaves involve a doubling of frequency or a ratio of 2. A perfect fifth involves a ratio of 3/2, and a major third, a ratio of 5/4.
A good way to understand this is to consider a guitar string. If you place your finger lightly across the middle of a string (above the 12th fret) you will hear a harmonic which is an octave higher than the open string. The string vibrates in nodes, and by halving the vibrating length of the string, the frequency is doubled.
If you lightly place your finger at one-third the length of the string (above the 7th fret) you will hear an harmonic which is an octave plus a fifth (the fifth note of the diatonic scale) above the open string. You are dividing the vibrating length of the string into thirds, which triples the frequency. Divide that by 2 to bring it into the same octave (not an octave higher) and the ratio is 3/2, or a frequency 3/2 times that of the open string. You can continue this experiment by dividing the string into 4, 5, or more equal-length nodes. Each note will be a frequency which is a simple ratio of that of the open string.
Now consider a circle of fifths. Go to the fifth note of a scale, use that as the first note of the next scale and go to the fifth note of that scale, and repeat that for a total of 12 times (C to G to D to A, etc.) and you should get back to the original note but 7 octaves higher (at least on a piano if you had enough keys). But if you do the arithmetic it doesn’t quite add up. The first fifth would be 3/2 times the frequency of the first note; the second, 3/2 times 3/2; and finally the 12th would be (3/2)12 = 129.746 times the frequency of the first note. Seven octaves would be 27 = 128. That’s quite a noticeable difference to the ear. It would even be noticeable over just a few octaves.
To remedy this on a piano or other instrument with fixed notes (such as a fretted guitar) we could divide an octave into 1200 cents (units of frequency), so that each whole tone would be 200 cents and each semitone 100 cents (12 semitones = 1 octave or 1200 cents). We would then have an even-tempered scale.
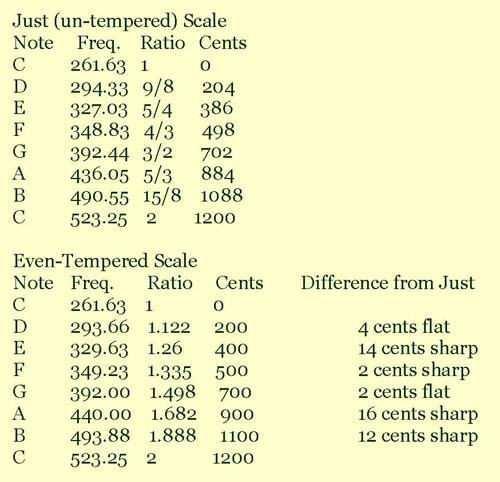
In the just or un-tempered (ideal) scale the interval between each semitone is slightly different. So if you started a melody in the key of C and then modulated to the key of G, for example, the fifth note (D) of that new key of G would be a slightly different ratio (not 3/2) in that scale and would not quite sound in tune. And the further we got from the original key of C the more out of tune it would sound. The even-tempered scale allows us to play in different keys on the same instrument by de-tuning each note slightly from the ideal so that the interval between each semitone is exactly the same.
In this even-tempered scale our fifth would be 700 cents, while in the just (un-tempered) scale it would be 702 cents. Most people can hear a difference of only about 5 cents or more, so this would not be noticed by the average person. However the major third is 400 cents in the even-tempered scale and 386 cents in the just; that is a noticeable difference. That is why our violin player sounds slightly flat to our piano player. The violin player can adjust her fingers to the ideal intervals while the piano player is restricted by the tuning of the keys. Whatever we are used to hearing sounds “normal” to our ears, and the piano player is used to hearing an even-tempered scale.
The following charts show the differences in frequency, ratios and cents for the two scales. Here it is assumed that middle C = 261.63 Hz for both, so that A = 440 Hz for the even-tempered scale.
Now go back to your guitar and play the harmonic with your finger lightly above the 4th fret (one-fifth of the length of the string). You should hear the ideal (un-tempered) major third, two octaves above the open string. Now press down on the 4th fret. If your guitar is perfectively adjusted you should hear an even-tempered major third above the open string, which should sound slightly sharp as compared to the un-tempered harmonic. It takes a good ear, but that can come with practice.
Singers and fretless string instrument players often unconsciously adjust their music to just intonation. Unaccompanied choirs and string ensembles tune their chords to perfect un-tempered intervals. That is the secret behind the unique sound of tight a capella harmony singing. Orchestras will often tune sustained chords to ideal intervals when instruments can bend their pitch to just intonation. In this video you can hear the difference in harmonies played in just and even-tempered scales. For a more detailed analysis of temperment see "How Equal Temperament Ruined Harmony (and Why You Should Care)" by Ross W. Duffin.
Now if I haven’t confused you too much with the math, you may understand why I prefer the violin to the piano, and why I am always tweaking my guitar tuning. It just sounds better to my ears.